经过前两期的专题训练,相信同学们对导数加三角这种题目的套路和处理方法逐渐清晰了,这种题目的难点在于分类讨论间断点的选择以及对导数,导函数,二阶导函数正负的判断,本身难度相比传统的导数题目反而有所降低,无论今年高考中会不会出现此类问题,建议都要掌握住此类问题的处理方法,文末也会对这三期内容的关键知识点作一次总结。
在处理恒成立的问题时,我习惯先判断端点值的函数值,导函数值和二阶导函数值,很多类似的题目其实用端点效应都能求的出来,另外恒成立问题先不急着分离参数,特别分离参数后发现后面的函数是分式形式且在端点值无意义,那么此类问题大概率会用到洛必达法则,而洛必达法则在高考中会扣除一部分分数,整体分类讨论的步骤会繁琐一些,很容易重和漏,这种题目见仁见智吧。


若分类讨论,函数无法直接判断单调性三角函数的导数,导函数中有恒正的对勾函数部分,且参数a与余弦值相乘,余弦函数在给定区间内的值域为(-1,1),所以讨论点就很清楚了,题目很常规,也很有代表性。

本题目把定义域拆成两部分,单调性和极大值很容易判定出来,在用隐零点处理最大值时注意其中的化简过程,将最大值表达式中的三角函数换成x,因此需要判断原来x0所在的区间范围是不是符合要求,题目让证明最大值小于2,若x0所处区间的最大值为π,显然最大值不可能小于2,将区间的右侧缩小即可,无需考虑区间的左侧,题目是一个典型的隐零点问题,后面第四题也是相似的隐零点问题。

注意上面h'(x)符号的判定无需再用二阶导,通过给定的区间即可判断出正负
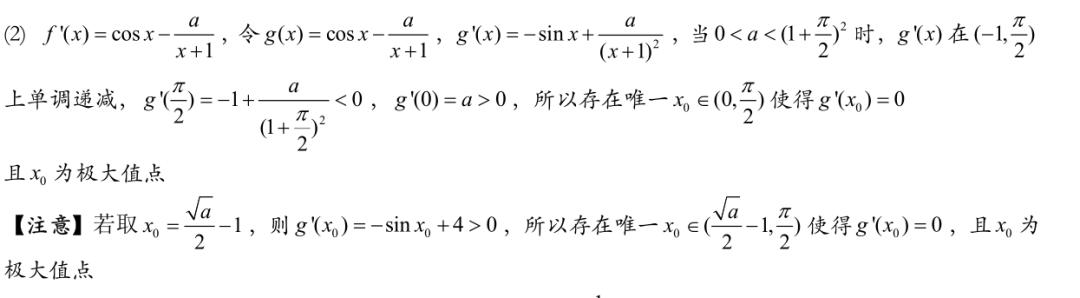
第二问选点很容易,注意上方过程最后的选点是根据什么来的

第三问是最常见的题型和最常见的分段处理零点问题的过程,和2019年全国卷理科数学很类似,这里需要提一下,一般而言原函数的单调性并不能直接看出,求导函数时有的导函数可根据题目的形式和给定的区间能直接判断出正负出来,有的导函数还能根据函数增减性的加减运算直接判定出来,若都不能,再求二阶导。


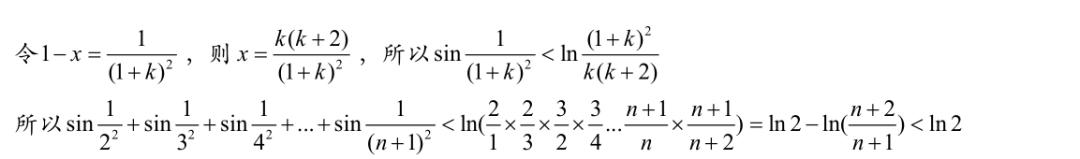
第二问这种累加型不等式的证明需要根据第一问的结论得到一个可直接使用的不等关系,题目很常见了,另外还有左右两侧都是累加型的情况,可用处理数列的方式来处理,第三问与三角无关,是一个常见的隐零点问题。

注意上面过程中为什么把x0的范围进一步缩小了,因为m可用x0表示出来,且m为负值,可求出x0的具体范围。
总结三期内容,三角加导数问题的处理难点和方法有以下几种:
难点1.函数,导函数,二阶导函数符号的判定
难点2.分类讨论的间断点选择问题
处理此类问题的常用技巧:
1.先确定区间端点的函数值,导数值和二阶导函数值
2.函数、导函数正负判定时可把区间拆分成容易判定符号的部分,逐个判定,或者利用给定区间函数的值域来判定,再或者直接利用三角函数中仅有的几个放缩法来判定。
3.关于导函数和二阶导函数单调性的判定,首先考虑函数运算中单调性的判断方法,即在特定区间内增函数+增函数,增函数-减函数,减函数+减函数,如不能判断,再用导数判定。
4.分类讨论时,时刻注意参数的位置以及参数变化对函数,导函数,二阶导函数值变化的影响,这种技巧是通过大量训练逐渐掌握的一种能力,需要仔细细心。
希望通过这三期内容,会让你对三角加导数的题目有一个大概的认识,遇见时不至于不知如何下手。
会员全站资源免费获取,点击查看会员权益