接龙(chain)
题目描述:
在玩惯了成语接龙之后,小 J 和他的朋友们发明了一个新的接龙规则。
总共有 n 个人参与这个接龙游戏,第 i 个人会获得一个整数序列 Si 作为他的词库。一次游戏分为若干轮,每一轮规则如下:
• n 个人中的某个人 p 带着他的词库 Sp 进行接龙。若这不是游戏的第一轮,那么这一轮进行接龙的人不能与上一轮相同,但可以与上上轮或更往前的轮相同。
• 接龙的人选择一个长度在 [2, k] 的 Sp 的连续子序列 A 作为这一轮的接. 龙. 序. 列. ,其中 k 是给定的常数。若这是游戏的第一轮,那么 A 需要以元素 1 开头,否则A 需要以上一轮的接龙序列的最后一个元素开头。
– 序列 A 是序列 S 的连续子序列当且仅当可以通过删除 S 的开头和结尾的若干元素(可以不删除)得到 A。
为了强调合作,小 J 给了 n 个参与游戏的人 q 个任务,第 j 个任务需要这 n 个人进行一次游戏,在这次游戏里进行恰好 rj 轮接龙,且最后一轮的接龙序列的最后一个元素恰好为 cj。为了保证任务的可行性,小 J 请来你判断这 q 个任务是否可以完成的,即是否存在一个可能的游戏过程满足任务条件。
输入:
从文件 chain.in 中读入数据。
本. 题. 有. 多. 组. 测. 试. 数. 据。.
输入的第一行包含一个正整数 T,表示数据组数。
接下来包含 T 组数据,每组数据的格式如下:
第一行包含三个整数 n, k, q,分别表示参与游戏的人数、接龙序列长度上限以及任务个数。
接下来 n 行:
第 i 行包含 (li + 1) 个整数 li , Si,1, Si,2, · · · , Si,li,其中第一个整数 li 表示序列 Si 的长度,接下来 li 个整数描述序列 Si。
接下来 q 行:
第 j 行包含两个整数 rj , cj,描述一个任务。
输出:
输出到文件 chain.out 中。
对于每个任务:输出一行包含一个整数,若任务可以完成输出 1,否则输出 0。
【样例 1 解释】
在下文中,我们使用 {Ai} = {A1, A2, · · · , Ar} 表示一轮游戏中所有的接龙序列,{pi} = {p1, p2, · · · , pr} 表示对应的接龙的人的编号。由于所有字符均为一位数字,为了方便我们直接使用数字字符串表示序列。
• 对于第一组询问,p1 = 1、A1 = 12 是一个满足条件的游戏过程。
• 对于第二组询问,可以证明任务不可完成。注意 p1 = 1、A1 = 1234 不是合法的游戏过程,因为此时 |A1| = 4 > k。
• 对于第三组询问,{pi} = {2, 1}、{Ai} = {12, 234} 是一个满足条件的游戏过程。
• 对于第四组询问,可以证明任务不可完成。注意 {pi} = {2, 1, 1}、{Ai} = {12, 23, 34}不是一个合法的游戏过程,因为尽管所有的接龙序列长度均不超过 k,但第二轮和第三轮由同一个人接龙,不符合要求。
• 对于第五组询问,{pi} = {1, 2, 3, 1, 2, 3}、{Ai} = {12, 25, 51, 12, 25, 516} 是一个满足条件的游戏过程。
• 对于第六组询问,可以证明任务不可完成。注意每个接龙序列的长度必须大于等于 2,因此 A1 = 1 不是一个合法的游戏过程。
• 对于第七组询问,所有人的词库均不存在字符 7,因此任务显然不可完成。
【数据范围】
对于所有测试数据,保证:
• 1 ≤ T ≤ 5;
• 1 ≤ n ≤ 10^5,2 ≤ k ≤ 2 × 10^5,1 ≤ q ≤ 10^5;
• 1 ≤ li ≤ 2 × 10^5,1 ≤ Si,j ≤ 2 × 10^5;
• 1 ≤ rj ≤ 10^2,1 ≤ cj ≤ 2 × 10^5;
• 设 ∑l 为单. 组. 测. 试. 数. 据. 内. 所有 li 的和,则 ∑l ≤ 2 × 10^5。
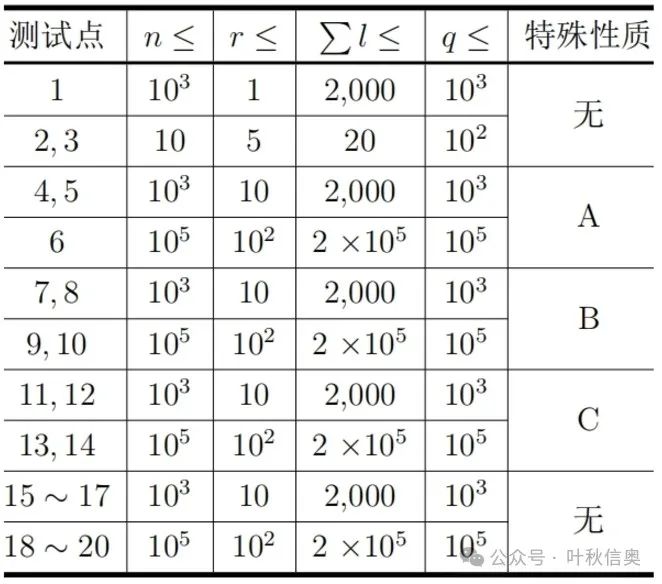
特殊性质 A:保证 k = 2 × 10^5。
特殊性质 B:保证 k ≤ 5。
特殊性质 C:保证在单组测试数据中,任意一个字符在词库中出现次数之和均不超过 5。
题解:
大胆猜测DP方程dp(i,j)表示当第i轮游戏结束时,以数字j结尾的情况。但具体记录什么情况呢?似乎遇上了困难。因为要满足条件”连续两轮游戏的玩家不能相同”,所以需要记录第i轮玩家的所有可能的集合。
但这样做会带来非常大的冗余,并且发现当集合的大小大于等于2时,就没有必要记录集合的元素了,因为在之后的转移中对于任意结尾元素x,都能在集合里找到另一个不相等元素y。
因此也只有集合中恰好有一个元素时值得记录答案si开头的成语,其他情况可以用两个用不到的数字替代,例如−1,−2。在次我选择用−1代表集合为空,−2代表集合中有至少两个元素。
对于转移,假设当前是第cnt轮游戏,DP方程由第cnt−1转移过来。需要遍历所有人的词库,当遍历到第i个人词库时,先找到第一个dp(cnt−1,x)不为−1的s[i][j] ,在这之后的所有数字都可以被转移到。
考虑k带来的限制后,发现对于s[i][j]需要维护一个下标lst,满足j−lst+1≤k 并且从dp(cnt−1,s[i][j])转移到dp(cnt,s[i][j])是合法的。对于lst即时更新即可。
AC代码:
#includeusing namespace std;const int INF=1e9;const int N=2e5+5;int t,n,k,q,r,c,len;void solve(){scanf("%d%d%d",&n,&k,&q);vector<vector<int>> dp(100+1,vector<int>(N,-1));vector<vector<int>> s(n+1);dp[0][1]=-2;for(int i=1;i<=n;i++){scanf("%d",&len);s[i].resize(len);for(int v=0;v<len;v++)scanf("%d",&s[i][v]);}for(int cnt=1;cnt<=100;cnt++){for(int i=1;i<=n;i++){int lst=-1;for(int j=0;j<s[i].size();j++){int x=s[i][j];if(lst!=-1 && (j-lst+1)<=k){if(dp[cnt-1][s[i][lst]]!=-1 && dp[cnt-1][s[i][lst]!=i]){if(dp[cnt][x]==-1)dp[cnt][x]=i;else if(dp[cnt][x]!=i)dp[cnt][x]=-2;}}int v=dp[cnt-1][x];if(v!=-1 && v!=i){lst=j;}}}}while(q--){scanf("%d%d",&r,&c);printf("%dn",dp[r][c]!=-1?1:0);}}int main(){scanf("%d",&t);while(t--){solve();}}
会员全站资源免费获取,点击查看会员权益