巧求三角面积。
一起来看一下小学五年级奥数题当中通过线段和面积的相互转化,最终求图形面积的问题。
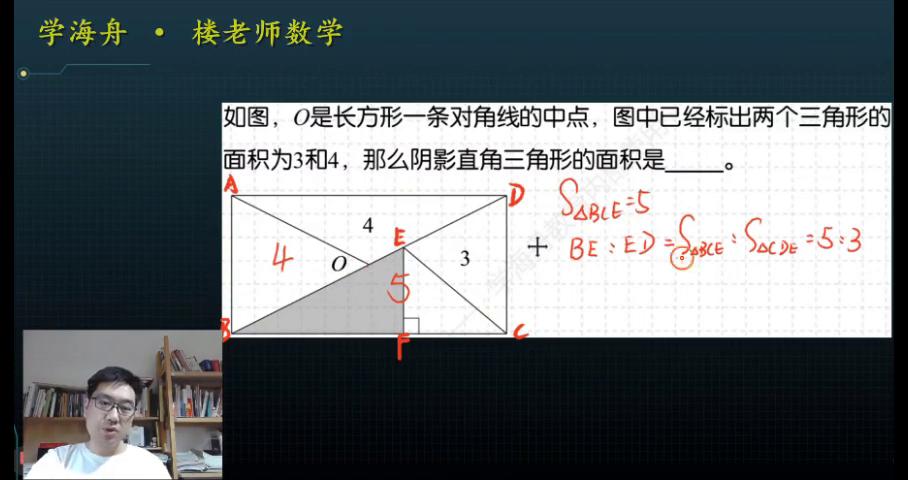
如图,o是长方形一条对角线的中点,图中已经标出两个三角形的面积为3和4,阴影直角三角形的面积是多少?因为o是长方形的中点,因此可以推断出三角形abo和三角形aod这两个三角形是等底等高的两个三角形,所以三角形abo的面积也应该是4。
现在这两个三角形面积加起来的和就是8分,这个8正好占了长方形面积的一半,因此另外一半也就是bcd,这个直角三角形的面积也应该是8,因为cde的面积是3,所以bce的面积就应该是5。

当三角形bce的面积知道,ed的面积也知道,在这种情况下因为它们的高度是相同的,所以面积的比就是线段的比。反过来线段直角三角形的面积公式,b e比上ed也就是三角形bce的面积比上三角形cde的面积也就是5比3。
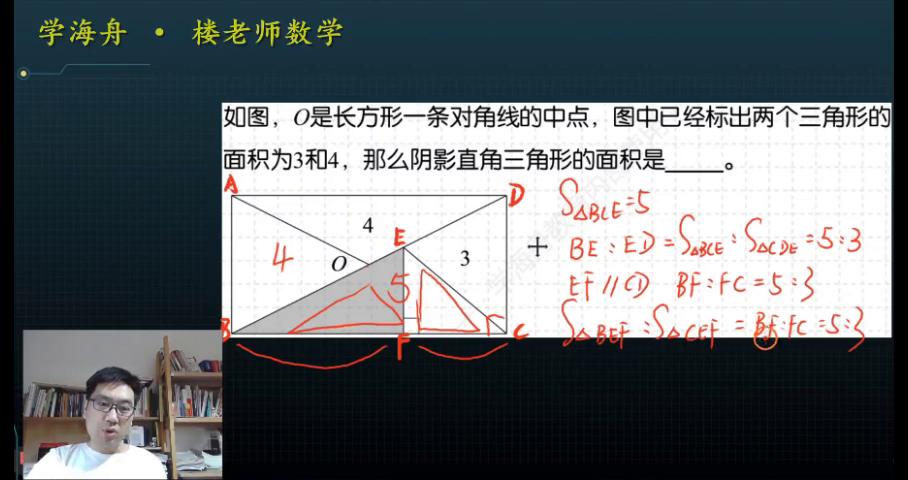
因为ef和dc都是垂直于bc的,这都是直角,所以ef负是平行于cd的,因此就知道ef比上fc也是5比3。三角形ef这个阴影部分和旁边三角形efc是等高三角形,所以两个的面积比就应该是底边长度的比,也就是三角形ef的面积比上三角形cef的面积就等于bf比上fc就是5比3。

因为大一点的三角形bce整体的面积刚刚求出来是5了,所以阴影部分的面积就应该是整个大三角形的面积,就是bce的面积乘上5加3分之1,它占了5分也就是8分之25。
这就是这个题的答案。
关注我,学习数学不上火,记得点赞关注。
会员全站资源免费获取,点击查看会员权益
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。