前些天有人发一篇文章,说在高考的数学复习题中,曾出现这样一道数学题:已知直角三角形ABC的BC直角边长是31,求这个三角形的面积。很多同学认为给的已知条件太少,无法求出面积。可有个学霸竟根据勾股定理的原理,依据勾的平方+股的平方=弦的平方,经过一系列演算,竟求出这个三角形的面积是7440。从演算过程看,发文者信誓旦旦!而认为根本不可能的却大有人在!那么,这种超常的计算方法到底可行吗?
一),我们知道,在三角函数知识中,单纯知道三角形的角度,是无法计算并确定三角形的边长的!→因为三个角的度数都完全相同的三角形有大有小有无数个!因此,必须需要知道其中一条边的长度,然后根据正弦定理,才能准确求出该三角形各边的边长。
同样的道理,直角三角形的面积等于两条直角边相乘再被2除(S=1/2ab)。如果只知道一条直角边的边长,是无法求面积的!→但如果再知道一个锐角的度数!然后根据三角函数的正弦定理,就可求出另条直角边长,只有这样才能准确求出这个三角形的面积。
二),

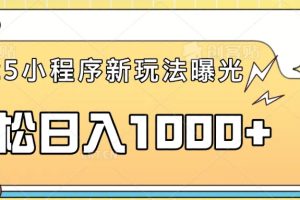
上图是笔者画的六个直角三角形!它们的直角底边→b边都设为31mm!而它们的另一直角边→a边,分别设为10㎜,15㎜,20㎜,25㎜,30㎜,35㎜,40㎜,45㎜,50㎜。很直观的看出:在直角三角形ABC中,由于角C度数的增加,它对应的a边的长度也在不断增加!进而使三角形的面积不断的扩大!例如
第三个三角形的面积是:
20×31÷2=310平方㎜
第七个三角形的面积是
40×31=620平方㎜
第九个三角形的面积是
50×31=775平方㎜
以上这些三角形的底边都是31㎜!但由于角C度数的大小直接影响a边的长短→因此出现了很多个底边虽然相同直角三角形的面积公式,但面积根本相同的很多个三角形!这就说明,只知道直角三角形其中一条直角边的数据,想准确求出这个三角形的面积,是不可能的。
我的水平确实有限,诚望有识之士参与讨论!以其得出明晰的结论。谢谢关注。
会员全站资源免费获取,点击查看会员权益